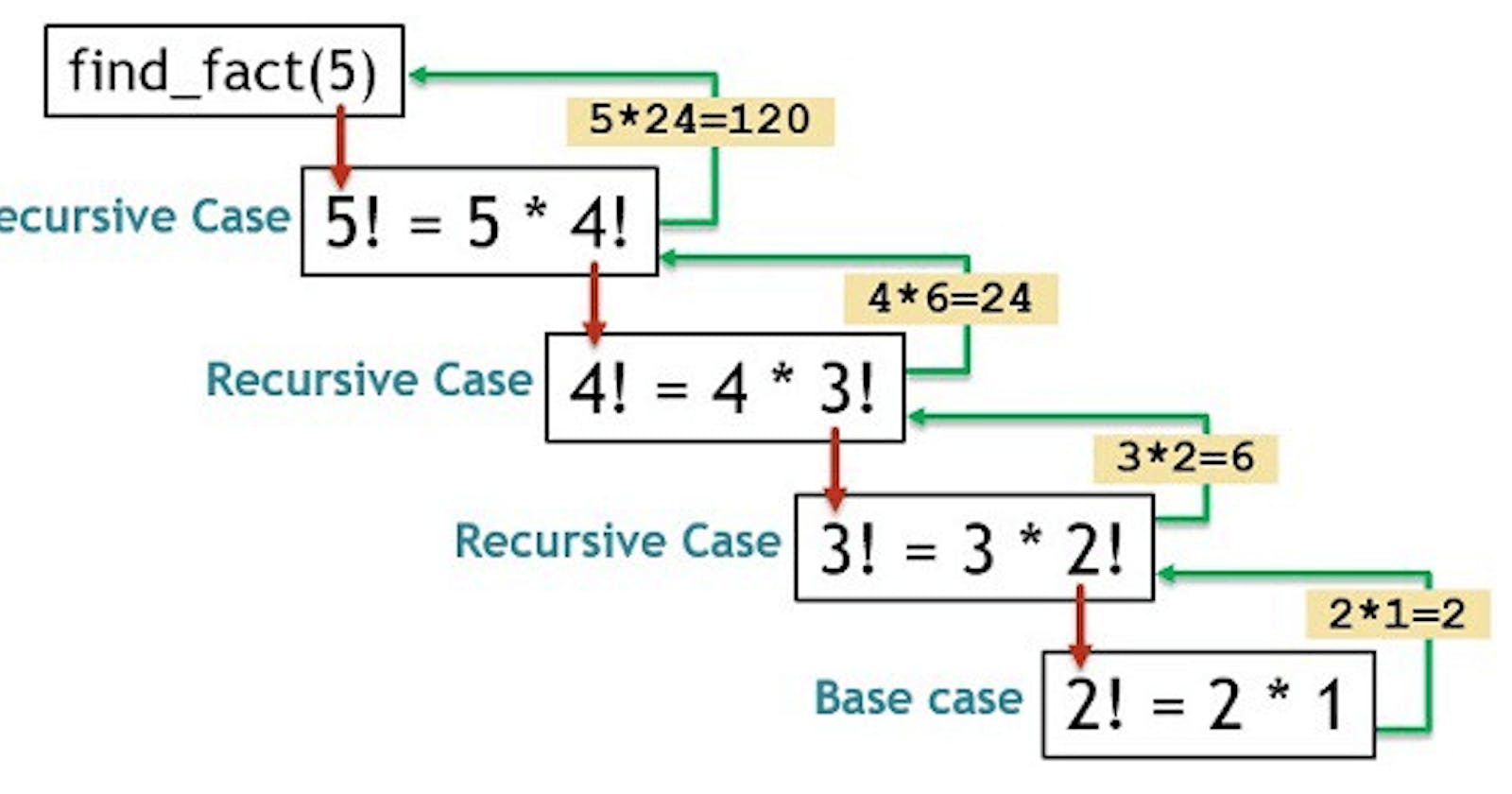
Recursion Approaches

Top down approach

1. return specific value for null node

2. update the answer if needed // answer <-- params

3. left_ans = top_down(root.left, left_params) // left_params <-- root.val, params

4. right_ans = top_down(root.right, right_params) // right_params <-- root.val, params

5. return the answer if needed // answer <-- left_ans, right_ans

Ex: Maximum depth of binary tree using top down

1. return if root is null
2. if root is a leaf node:
3.     answer = max(answer, depth)         // update the answer if needed
4. maximum_depth(root.left, depth + 1)     // call the function recursively for left child
5. maximum_depth(root.right, depth + 1)    // call the function recursively for right child

private int answer; // don't forget to initialize answer before call maximum_depth
private void maximum_depth(TreeNode root, int depth) {
    if (root == null){
        return ;
    }
    if (root.left == null && root.right == null) {
        answer = Math.max(ans, depth);
    }
    maximum_depth(root.left, depth+1);
    maximum_depth(root.left, depth+1);
}

Bottom-Up Solution

1. return specific value for null node
2. left_ans = bottom_up(root.left)      // call function recursively for left child
3. right_ans = bottom_up(root.right)    // call function recursively for right child
4. return answers                       // answer <-- left_ans, right_ans, root.val

1. return 0 if root is null                 // return 0 for null node
2. left_depth = maximum_depth(root.left)
3. right_depth = maximum_depth(root.right)
4. return max(left_depth, right_depth) + 1  // return depth of the subtree rooted at root

public int maximum_depth(TreeNode root) {
    if (root == null) {
        return 0;                                   // return 0 for null node
    }
    int left_depth = maximum_depth(root.left);
    int right_depth = maximum_depth(root.right);
    return Math.max(left_depth, right_depth) + 1;   // return depth of the subtree rooted at root
}

Symmetric Tree

Given the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).

 public boolean isSymmetric(TreeNode root) {

        return isMirror(root,root);
    }

    public boolean isMirror(TreeNode t1, TreeNode t2) {

        if (t1 == null && t2 == null) return true;
        if (t1 == null || t2 == null) return false;

        return (t1.val == t2.val) && isMirror(t1.right, t2.left) && 
        isMirror(t1.left, t2.right);
    }

Has Path Sum in Tree

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

public boolean hasPathSum(TreeNode root, int targetSum) {

       if (root == null){
           return false;
       }
       int sum = targetSum - root.val;
       if (root.left == null && root.right == null) {
           return sum == 0;
       } 
       return hasPathSum(root.left, sum) || hasPathSum(root.right, sum);

    }

Principle of Recursion

A recursive function should have the following properties so that it does not result in an infinite loop:

1. A simple base case (or cases) — a terminating scenario that does not use recursion to produce an answer.

2. A set of rules, also known as recurrence relation that reduces all other cases towards the base case.

Print a string in reverse order

private static void printReverse(char [] str) {
  helper(0, str);
}

private static void helper(int index, char [] str) {
  if (str == null || index >= str.length) {
    return;
  }
  helper(index + 1, str);
  System.out.print(str[index]);
}

Reverse a Linked list

public ListNode reverseList(ListNode head) {
        if (head == null || head.next == null) {
            return head;
        }

        ListNode reversedSubList = reverseList(head.next);
        head.next.next = head;
        head.next = null;
        return reversedSubList;
    }

Reverse a Linked List Iterative

 public ListNode reverseList(ListNode head) {
        ListNode prev = null;
        ListNode curr = head;
        while (curr != null) {
            ListNode nextTemp = curr.next;
            curr.next = prev;
            prev = curr;
            curr = nextTemp;
        }
        return prev;
    }

Search in Binary Tree

public TreeNode searchBST(TreeNode root, int val) {

        if (root == null || root.val == val) {
            return root;
        }
        if (val < root.val) {
            return searchBST(root.left, val);
        }

        return searchBST(root.right, val);

    }

Fibonacci with Memoization

class Solution {

    HashMap<Integer, Integer> cache = new HashMap<>();
    public int fib(int n) {
        if (n==0) {
            cache.put(0, 0);
            return 0;
        }
        if (n==1) {
            cache.put(1,1);
            return 1;
        }
        if (cache.containsKey(n)) {
            return cache.get(n);
        }
        int result = fib(n-1) + fib(n-2);
        cache.put(n, result);
        return result;
    }
}

Climbing Stairs

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

class Solution {
    private HashMap<Integer, Integer> map = new HashMap<>();
    public int climbStairs(int n) {  
        if (n == 0) {
            map.put(0,0);
            return 0;
        }
        if (n==1) {
            map.put(0,0);
            return 1;
        }
        if (n==2) {
            map.put(0,0);
            return 2;
        }

        if(map.containsKey(n)) {
            return map.get(n);
        }

        int result =  climbStairs(n-1) + climbStairs(n-2);

        map.put(n, result);
        return result;

    }
}